|
Mandelbr displays the Mandelbrot set.
The Mandelbrot set is a set of points in the complex plane. In the
complex plane the real part of a complex number is represented
along the x-axis, and the imaginary part along the y-axis. A point
z[0] in the complex plane is member of the Mandelbrot set, if
the sequence z[n+1] := z[n] ** 2 + z[0] (for n >= 0) is bounded.
That is, a complex number, z[0], is in the Mandelbrot set if, when
applying the iteration repeatedly, the absolute value of z[n]
never exceeds 2. If the absolute value of any z[n] becomes larger
than 2, the sequence will escape to infinity. The boundary of
the Mandelbrot set forms a fractal.
The points of the Mandelbrot set are displayed in black.
For unbounded points the number of the iteration n, for which
abs(z[n]) >= 2.0 holds, is mapped to a color. For practical
purposes the program limits the iterations to a maximum of
256 and assumes that a point is member of the Mandelbrot set
if reaching this limit.
The program accepts the following mouse commands:
- The left mouse key selects a new center and magnifies by factor 2.
- The middle mouse key selects a new center.
- The right mouse key scales down by factor 2.
The following keyboard commands are also accepted: Help, Restart and Quit.
|
|
Welcome screen |
|
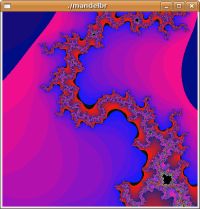
Spiral |
|
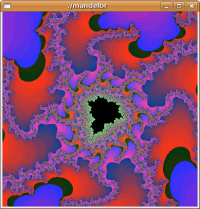
Self-similar |
|
|

